ÉCONOMÉTRIE

ÉCONOMÉTRIE

Les économistes s’efforcent d’établir des relations entre les variables qui décrivent et mesurent les phénomènes et comportements qu’ils étudient. L’économétrie se définit par l’application des méthodes de l’induction statistique en vue de vérifier ces relations suggérées par la théorie économique, d’estimer numériquement leurs paramètres et de construire à partir d’elles des modèles économiques chiffrés. L’économétrie se distingue ainsi de l’économie mathématique (qui étudie des relations entre variables économiques sans préciser les valeurs numériques des paramètres) et des statistiques économiques descriptives (qui mesurent des variables économiques sans chercher à établir des relations entre elles).

C’est la combinaison des méthodes mathématiques, de la théorie économique et des données statistiques qui donne à l’économétrie son efficience. En utilisant ses méthodes, il est possible de démontrer le caractère irréaliste, ou tout au moins inadéquat, d’une théorie économique; de montrer, à l’inverse, son adéquation aux faits et de lui donner une valeur opératoire en chiffrant les relations qu’elle suggère; et enfin, de préciser l’imprécision qui affecte ces estimations numériques. De ce dernier point de vue, on peut dire que l’économétrie est l’art d’analyser et de quantifier les erreurs.

À la base de l’économétrie, on trouve la théorie de la régression dont les applications dépassent le champ de l’économie puisqu’elles peuvent concerner tout traitement de données statistiques. Mais l’objectif de l’économétrie est la construction de modèles économiques. Ces derniers peuvent être construits et utilisés par des entreprises, tandis que les modèles macro-économiques aident les administrations à définir la politique économique nationale à travers la prévision de la conjoncture, les budgets économiques et la planification.

Théorie des régressions

La méthode des régressions, dans ses applications à l’économie, vise à concilier deux objectifs contradictoires: d’une part, les mécanismes économiques sont infiniment complexes et leur représentation exacte exigerait un très grand nombre de variables et de relations; d’autre part, un modèle, pour être utilisable, doit être simple. En outre, la plupart des variables économiques sont mesurées avec des erreurs. À titre de compromis, on introduit dans les relations économétriques une variable aléatoire 﨎, appelée erreur, ou résidu, qui représente la somme de tous les effets non pris en compte et des éventuelles erreurs de mesure. On écrira donc:

où les x ⁱ sont appelées variables exogènes (explicatives) et y variable endogène (expliquée).

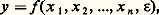Régression simple

La régression simple est une relation qui ne fait intervenir qu’une seule variable explicative. On peut ramener cette relation à une forme linéaire, quitte à remplacer les variables économiques observées par des fonctions de ces variables (par exemple leurs logarithmes). On écrit donc:

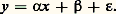Cette relation devient une régression lorsqu’on fait des hypothèses sur la loi de la variable aléatoire 﨎. Par exemple, si les facteurs non pris en compte sont nombreux, indépendants et du même ordre, on fera l’hypothèse que l’erreur 﨎 suit une loi de Gauss.

Ces prémisses étant posées, le problème de la régression est le suivant: à partir de n couples d’observations (x ⁱ , y ⁱ ) qui peuvent correspondre à différentes périodes, différents secteurs de production ou différents pays, et des hypothèses faites sur la loi de distribution du terme d’erreur 﨎, comment estimer au mieux les paramètres 見 et 廓? On est ainsi ramené à un problème d’estimation statistique.

La méthode d’estimation, très souvent utilisée en pratique, est celle des moindres carrés. Elle consiste à choisir pour droite d’ajustement (comme approximation de la droite théorique inconnue) la droite D, d’équation y = ax + b , telle que la somme des carrés des distances à D, mesurées parallèlement à Oy , soit minimale. Cette droite passe par le point moyen du nuage de points, de coordonnées:

et ses paramètres a et b , estimateurs de 見 et 廓, se calculent aisément (cf. figure).

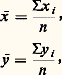L’utilisation très générale du critère des moindres carrés se justifie par les propriétés des estimateurs a et b , propriétés intéressantes, même avec des hypothèses faibles sur la variable aléatoire 﨎. En particulier, les paramètres a et b de la droite des moindres carrés sont des estimateurs centrés des paramètres 見 et 廓 de la droite théorique. Sous des hypothèses plus fortes, on démontre que a et b sont des estimateurs convergents et efficaces. Ces hypothèses garantissent ainsi que la droite des moindres carrés est l’ajustement théoriquement le meilleur. Elles permettent en outre de préciser l’imprécision de l’ajustement, ce qui est important en pratique, tout en étant l’essence même de la méthodologie économétrique. Il est en effet possible de préciser la loi statistique (ou une loi approchée) que suivent les estimateurs a et b . On calcule en particulier l’écart type de ces paramètres (plus précisément, l’estimation de leur écart type). Ces valeurs sont généralement écrites entre parenthèses sous celles des paramètres estimés. À partir d’elles, on peut déterminer un intervalle de confiance pour les valeurs calculées de a et b .

On fait souvent figurer aussi, à côté de l’équation de régression, la valeur du coefficient de corrélation ou son carré, R², qui est la fraction de la variance de y expliquée par la régression. Il est cependant difficile de juger de la qualité d’un ajustement à partir de cette valeur, car elle dépend du nombre d’observations.

Tous ces résultats ne sont valables que si les hypothèses faites ne s’écartent pas trop de la réalité. Deux difficultés principales peuvent les remettre en cause: l’autocorrélation des résidus et les erreurs sur les variables.

Il y a autocorrélation des résidus lorsque les valeurs successives 﨎ⁱ ne sont pas statistiquement indépendantes. Ce cas se produit fréquemment avec les séries temporelles qui décrivent l’évolution d’une variable économique. L’évaluation des écarts types ainsi que les tests de signification sont alors incorrects. Pour détecter l’autocorrélation, on utilise généralement le test de Durbin et Watson, fondé sur une quantité appelée rapport de Von Neumann, dont la loi de distribution est fournie par des tables. Comme l’autocorrélation peut signifier une erreur dans la forme de la relation ou l’oubli d’une variable qui influence significativement y , il faut rechercher d’autres ajustements jusqu’à ce que l’indépendance des résidus soit retrouvée.

Lorsque les deux variables x ⁱ et y ⁱ sont mesurées avec erreur, les estimations des moindres carrés sont biaisées et non convergentes. On utilise dans ce cas une méthode dite des variables instrumentales qui consiste à recourir à une troisième variable, fortement corrélée avec x ⁱ et y ⁱ , mais indépendante des erreurs sur ces variables.

Régression multiple

Une régression sur une seule variable explicative n’étant généralement pas suffisante, on est conduit à introduire plusieurs variables explicatives x ¹ ... x ^k . La relation:

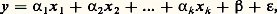est ainsi estimée par l’équation des moindres carrés:

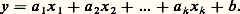Sous les hypothèses faites pour la régression simple, on retrouve, pour les paramètres de cet hyperplan des moindres carrés, les propriétés d’absence de biais, de convergence, d’efficacité... Les tests de signification de chaque variable peuvent être construits comme précédemment.

Cependant, une difficulté spécifique aux régressions multiples surgit quand les variables explicatives sont fortement corrélées entre elles. On parle alors de multicollinéarité . Dans ce cas, la méthode de calcul des coefficients des moindres carrés devient imprécise.

La collinéarité est malheureusement fréquente en macro-économie. Si, par exemple, on veut expliquer le niveau des importations d’un pays par celui du produit intérieur brut et celui de la consommation des ménages (ce qui est logique d’un point de vue économique), on observe que ces deux variables explicatives varient très sensiblement de façon parallèle (parce que la consommation constitue une part importante du produit intérieur, part qui est de plus stabilisée par la politique économique).

La collinéarité est souvent détectée par des écarts types élevés des coefficients de régression qui cessent d’être significatifs. Lorsque d’éventuelles collinéarités sont suspectées, une analyse systématique est nécessaire: on examine toutes les régressions concevables en introduisant ou rejetant de nouvelles variables, en fonction des tests de signification qu’il est possible de faire. Mais les variables qui ne sont pas introduites pour des raisons de collinéarité et qui n’améliorent pas la qualité économétrique de l’ajustement ont parfois une signification économique qui ne doit pas être oubliée quand on interprète les résultats: on ne doit pas dire que les variables omises n’ont pas d’effet, mais seulement que cet effet ne peut être isolé de celui des variables retenues. Cela signifie encore que la collinéarité est gênante pour l’estimation individuelle des effets de chaque facteur, mais qu’elle l’est beaucoup moins quand on recherche une prévision de la valeur de la variable endogène, à la condition que la collinéarité du passé se maintienne dans l’avenir, c’est-à-dire que les variables non prises en compte continuent d’être convenablement représentées par les variables explicatives introduites.

D’autres problèmes sont posés par l’introduction de la variable temps. En particulier, il arrive souvent que des variables caractérisant des périodes passées influencent la variable endogène de la période présente. Le nombre des facteurs explicatifs risque alors d’être excessif au regard des données disponibles. On cherche dans ce cas à effectuer une transformation de variables pour en réduire le nombre.

Exemple : beaucoup de travaux économétriques ont été consacrés à la fonction de consommation introduite initialement par Keynes et qui joue un rôle central dans l’analyse macro-économique. Sous sa forme la plus simple, cette fonction de consommation s’écrit:

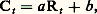où C^t et R^t sont respectivement la consommation globale et le revenu disponible des ménages pendant la période t . Cette relation s’est révélée rapidement trop schématique. Diverses théories économiques – notamment la théorie dite du «revenu permanent» – permettent de supposer que la consommation globale des ménages (annuelle ou trimestrielle) dépend non seulement des revenus perçus par ces ménages pendant la période présente, mais aussi des revenus des périodes passées. Si l’on suppose que l’influence de ces revenus passés décroît géométriquement avec le temps, selon le modèle:

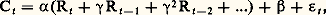on peut écrire la forme équivalente:

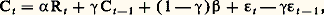modèle dit autorégressif (à cause de la variable endogène retardée jouant le rôle de variable exogène) qui ne fait plus intervenir que deux variables explicatives.

Modèles économétriques

Les premières analyses économétriques ne visaient qu’à établir une seule équation, tandis qu’aujourd’hui elles aboutissent à la construction de systèmes de plusieurs équations (parfois des milliers) appelés modèles économétriques (ou parfois modèles économiques).

Construction

La construction de tels modèles exige une analyse du système à modéliser et un ensemble important de données statistiques. En outre, l’estimation de l’ensemble des équations pose des problèmes spécifiquement économétriques.

Tant que, dans l’ensemble des relations, une variable endogène ne réapparaît pas comme variable exogène, les relations peuvent être estimées successivement sans difficulté. Dans le cas contraire, l’hypothèse que les variables explicatives ne sont pas aléatoires n’est plus satisfaite, et les méthodes d’estimation précédentes ne sont plus applicables. Il faut alors faire en sorte que les variables endogènes n’apparaissent plus comme variables explicatives. Il suffit pour cela de résoudre le système directement suggéré par l’analyse économique (appelé forme structurelle du modèle) par rapport aux variables endogènes. Le modèle est alors mis sous sa forme réduite et il est possible d’en estimer les coefficients. Comme cependant la connaissance des coefficients structurels, qui sont les seuls à être d’interprétation et d’utilisation faciles, est souvent indispensable, il faut pouvoir passer des coefficients de la forme réduite aux coefficients structurels, ce qui n’est pas, dans le cas général, possible et pose un problème d’identification .

Lorsqu’il est impossible de déduire, d’une forme réduite estimée, une forme structurelle complètement déterminée, on dit que le système est sous-identifié. Il est identifié lorsqu’il est possible de déterminer sans ambiguïté sa forme structurelle à partir de sa forme réduite (méthode des moindres carrés indirects). Enfin, il est suridentifié quand il est impossible de remonter de la forme réduite à une forme structurelle qui vérifie certaines contraintes connues a priori. Dans ce cas, on utilise une application particulière de la méthode des variables instrumentales, introduite par Theil et connue sous le nom de méthode des doubles moindres carrés .

Exemple : le modèle économique de Keynes, sous sa forme la plus simple,

Au contraire, le modèle légèrement modifié suivant est sous-identifié: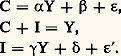

En effet, les deux premières équations permettent d’écrire (première équation de la forme réduite précédente):

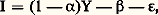équation qui est de la même forme que la troisième équation du système dont elle ne peut donc pas être distinguée.

Traiter l’investissement comme une variable exogène suffit donc à rendre le modèle identifié, mais ce traitement est bien sommaire d’un point de vue économique. L’hypothèse faite dans le second modèle est plus satisfaisante, mais c’est alors le traitement statistique qui pose des difficultés, puisque seule la forme réduite peut être estimée.

Structures et types de modèles économétriques

Les relations qui constituent un modèle ne sont pas toutes des ajustements économétriques. Un modèle est généralement composé:

– d’équations de définition , qui précisent un concept;

– d’équations comptables , d’autant plus nombreuses qu’on utilise un cadre comptable cohérent et complet tel que la comptabilité nationale. Elles donnent au modèle plus de précision et de stabilité;

– d’équations fonctionnelles , qui constituent le cœur du modèle. Elles sont obtenues par analyse des réalités techniques, institutionnelles et surtout par estimation statistique selon les méthodes exposées antérieurement.

Comme précédemment, mais au niveau du modèle tout entier et non plus du modèle que constitue une équation économétrique isolée, on distingue les variables endogènes et les variables exogènes. Les premières sont considérées comme déterminées par le phénomène que le modèle traduit. Les secondes sont données indépendamment du modèle par une autre étude ou fixées par une instance de décision. Dans ce dernier cas, on les appelle variables de commande .

Un modèle peut donc s’écrire symboliquement:

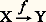f étant l’ensemble des opérations permettant de calculer les variables endogènes Y à partir des variables exogènes X.

À travers le modèle qui le représente, on peut ainsi étudier un système économique (entreprise, secteur de production, économie nationale) et en particulier prévoir son évolution.

On oppose parfois les modèles descriptifs (ou empiriques) aux modèles analytiques (ou théoriques). Les premiers décrivent les réactions du système étudié sans les expliquer et leurs prévisions reposent sur l’hypothèse de persistance des conditions prévalant pendant la période qui a permis d’estimer leurs paramètres. C’est le cas, par exemple, de l’analyse des séries temporelles selon des modèles autorégressifs développés par G. Box et G. Jenkins (1970). Au contraire, un modèle analytique essaie de décrire le fonctionnement réel du système qu’il représente par des relations de causalité. En pratique, des modèles mixtes qui combinent les deux approches sont utilisés. C’est le cas en particulier des modèles macro-économiques utilisés dans les études de politique économique. Ces modèles font intervenir des agrégats (production d’une branche, consommation globale des ménages, etc.) entre lesquels existent des relations d’interdépendance qui ne peuvent pas être complètement explicitées en termes de causalité.

Au-delà de la simple prévision, la plupart des modèles permettent d’étudier les réactions d’un système à d’éventuelles décisions, prises en compte à l’aide des variables de commande. En attribuant à ces variables diverses valeurs, le modèle décrit les évolutions correspondantes. Si le choix entre ces possibilités est effectué en cherchant le maximum d’une fonction d’évaluation, le modèle est un modèle d’optimisation , permettant d’obtenir le développement optimal (au sens de la fonction d’évaluation retenue) du système sous contrôle. Cette démarche constitue le principe des méthodes de programmation qui ont largement contribué au développement des modèles d’entreprise. En macro-économie, cette approche n’a guère été utilisée que pour les modèles de développement à long terme et elle a donné naissance à la théorie des croissances optimales, dont les bases et les possibilités d’application sont cependant restées fragiles.

La décision peut être aussi le résultat d’un processus qui n’explicite pas a priori une fonction d’évaluation. Tel est le cas lorsqu’un choix politique intervient après l’examen d’un certain nombre de variantes décrites par le modèle, qui fonctionne alors en simulation . Dans la pratique actuelle, le choix des politiques économiques à court et à moyen terme est souvent éclairé par un tel examen organisé suivant une procédure itérative.

Application des méthodes économétriques

L’idée d’une étude quantitative d’un système économique est très ancienne puisqu’on la trouve chez Petty, Boisguillebert (1695), King (1696), Quesnay (1758)... Mais l’économétrie proprement dite n’apparaît qu’au début du XX^e siècle avec les travaux de Moore, Schultz, Working notamment. Dans un premier temps, les études économétriques ont eu pour objectif l’établissement d’une seule relation, notamment dans le domaine de l’analyse de la demande; ainsi, R. Benini, en 1907, estime l’élasticité par rapport au prix de la demande de café en Italie. À partir de 1920, la méthode des modèles unirelationnels a surtout été appliquée à la construction de baromètres économiques par de nombreux instituts de conjoncture et de prévision. Ces indices précurseurs, dont le plus célèbre fut le baromètre de Harvard (1920), différaient profondément des modèles d’aujourd’hui. Faute d’avoir été en mesure de prévoir la crise de 1929, le baromètre de Harvard fut abandonné et son échec mit en évidence, d’une manière définitive, l’insuffisance des modèles à une seule relation construits de façon totalement empirique.

Cependant, dans un autre domaine, la même méthode a été appliquée à l’analyse des fonctions de production avec les hypothèses de Cobb et Douglas (1928), tandis que Ramsey, la même année, jetait les bases théoriques des modèles de croissance.

À partir de ces premiers éléments et des leçons tirées des échecs rencontrés, la construction de modèles ayant un soubassement théorique et comportant plusieurs équations devient un problème central dès 1930, date de la fondation de la Société internationale d’économétrie. R. Frisch jouera un rôle important dans la création de cette société et de sa célèbre revue Econometrica . C’est à cette époque que le terme de modèle économétrique fut précisé, en faisant une distinction nette entre modèles théoriques et modèles empiriques. Par la suite, l’apport fondamental de J. M. Keynes (1936), ceux de Tinbergen (qui a été le premier à recevoir le prix Nobel d’économie en 1969) et de Harrod (1939) ont joué un rôle décisif dans l’élaboration de modèles complets décrivant les fluctuations de la production et apportant quelques éléments de réponse aux principales questions de politique économique. Ces apports seront prolongés par W. Leontief avec les modèles dits d’input-output qui retracent les relations interindustrielles. Ces progrès théoriques serviront de base aux modèles qui seront construits après la Seconde Guerre mondiale, lesquels se multiplieront et se perfectionneront, surtout grâce à l’amélioration des données statistiques et à l’établissement de systèmes cohérents de comptabilité nationale. En outre, les progrès du traitement informatique des données ont grandement facilité la construction et l’utilisation des modèles économétriques.

Aujourd’hui, l’utilisation de ces modèles s’est généralisée. D’une part, la plupart des grandes entreprises ont construit et utilisent des modèles spécifiques qui contribuent à améliorer leur gestion interne ou à prévoir l’évolution de leurs marchés. D’autre part, de très nombreuses organisations publiques et privées ont construit des modèles macro-économiques nationaux ou internationaux. Parmi ces modèles économiques d’ensemble, ceux qu’utilisent les gouvernements ont une importance particulière puisqu’ils contribuent à la définition des budgets économiques et des politiques à court terme ainsi que des plans à long et moyen terme. Pratiquement, tous les pays (quel que soit leur régime politique ou leur niveau de développement) disposent de modèles économétriques plus ou moins perfectionnés, fournissant des prévisions quant à l’évolution des principales variables économiques (production, prix, commerce extérieur, chômage, etc.) et permettant d’éclairer leurs choix de politique économique. Par ailleurs, des modèles tentant de décrire l’évolution mondiale ont sensibilisé l’opinion publique (ce fut notamment le cas du modèle Meadows [1972], patronné par le club de Rome) aux problèmes démographiques, alimentaires, énergétiques et écologiques que pose, à long terme, le développement économique.

Objectifs et limites des méthodes

Les méthodes économétriques ne peuvent évidemment pas cerner toutes les causalités mises en jeu dans un système économique complexe. D’ailleurs, ces méthodes ne sont généralement pas utilisées pour réaliser des représentations du système étudié, mais pour agir au mieux sur lui. Par exemple, on cherchera à réaliser les meilleures prévisions dans les domaines où l’intervention du décideur informé peut se révéler efficace et importante, quitte à se contenter de prévisions imprécises dans des domaines moins stratégiques. C’est dire que la mise en œuvre des méthodes économétriques ne peut se faire qu’à partir de l’analyse des objectifs poursuivis et en collaboration avec les instances de décision. Au-delà de l’amélioration des prévisions et des décisions économiques, qui constitue l’objectif principal des méthodes économétriques, le recours à ces méthodes présente de multiples avantages.

La nécessité d’une approche systématique, précise et quantifiée conduit souvent à poser certaines questions fondamentales qu’une approche non formalisée aurait négligées. Elle permet de capitaliser les connaissances et les résultats des expériences selon un processus d’apprentissage que ne permettent pas les démarches empiriques. Lorsqu’il est construit, un modèle économétrique peut également servir à mieux faire comprendre le fonctionnement du système modélisé ainsi qu’à fournir des pôles communs de discussion dans un processus de concertation des parties concernées par la décision.

En contrepartie de ces avantages, les méthodes de l’économétrie et l’utilisation des modèles en particulier présentent des limites qu’il importe de connaître pour éviter les erreurs de prévision et de gestion et, plus généralement, les effets négatifs d’une représentation partielle ou schématique de la réalité.

Il est tout d’abord évident que ces méthodes ne peuvent pas fournir de résultats valables si elles utilisent des données statistiques médiocres. Tout travail économétrique doit donc commencer par l’analyse de la qualité et de la signification de ces données. Par ailleurs, il arrive souvent que l’analyse économétrique donne trop de poids aux relations quantifiables et néglige les phénomènes qui ne sont pas mesurables ou qui échappent au traitement mathématique. En outre, la plupart des formalisations économétriques restent des «boîtes noires», c’est-à-dire qu’elles fournissent des sorties en réponse à des entrées sans qu’il soit possible d’éclairer toutes les relations de causalité entre les unes et les autres. Ne garantissant pas la qualité des relations causales, dans le domaine de la macro-économie notamment, les méthodes économétriques ne garantissent pas toujours la fiabilité des prévisions effectuées. Les phénomènes de collinéarité en particulier rendent vulnérables, à certains moments, des relations qui fournissent ordinairement de bons résultats. C’est pourquoi la prévision des points tournants et des inflexions brutales dans l’évolution d’un système reste très difficile et pratiquement hors de portée de ces méthodes. Certes, ces erreurs de prévision restent relativement rares, mais leurs conséquences peuvent être graves et, à la limite, de mauvaises méthodes économétriques conduisent à la situation suivante: quand la prévision est simple à effectuer, elle est inutile; quand elle est difficile et nécessaire, elle est fausse. De façon générale, et quelle que soit leur qualité technique, les approches économétriques sont fondées sur une hypothèse générale de permanence des mécanismes qui ont joué dans le passé et conduisent ainsi, par construction, à une vision relativement conservatrice du futur. Pour toutes ces raisons, il est toujours prudent de compléter les analyses économétriques par des méthodes non formalisées et plus qualitatives pour tenter de prendre en compte les aspects du système étudié qu’on ne sait pas mettre en équations.

économétrie [ ekɔnɔmetri ] n. f.

• 1949; de économie et -métrie

♦ Sc. Application de méthodes mathématiques et statistiques à l'étude et à la représentation de phénomènes économiques. — Adj. ÉCONOMÉTRIQUE , 1952 .

● économétrie nom féminin Méthode d'analyse des données économiques qui, par l'utilisation de la statistique, s'attache à établir des relations de caractère mathématique entre les phénomènes étudiés.

économétrie

n. f. Didac. Application des méthodes mathématiques aux sciences économiques.

⇒ÉCONOMÉTRIE, subst. fém.

Branche de l'économie qui traite par les mathématiques les données statistiques relatives aux phénomènes économiques afin d'en améliorer l'analyse ou d'en dégager des lois ou des relations constantes. Quant à l'économétrie, il allait de soi de consacrer le domaine de l'économique au nombre (Gds cour. pensée math., 1948, p. 394).

Rem. 1. Celui qui est spécialiste d'économétrie est l'économètre, subst. masc. (cf. Univers écon. et soc., 1960, p. 2216; Colloque géogr. appl., 1962, p. 82). 2. L'adj. correspondant est économétrique. Qui se rapporte à l'économétrie; qui concerne l'économétrie. Lois économétriques (Univers écon. et soc., 1960, p. 2416). Ce nouveau problème s'énonce à partir des données de l'observation statistique et, quand c'est possible, de l'enquête économétrique (PERROUX, Écon. XX^e s., 1964, p. 334).

Prononc. :[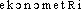]. Étymol. et Hist. 1948 (Gds cour. pensée math., p. 393). Dér. du rad. de économie; élément suff. -métrie (-mètre et -ie). Bbg. GIRAUD (J.), PAMART (P.), RIVERAIN (J.). Mots ds le vent. Vie Lang. 1970, p. 390.

économétrie [ekɔnɔmetʀi] n. f.

ÉTYM. 1949, in D. D. L.; de économie, et -métrie.

❖

♦ Sc. Traitement mathématique de données statistiques concernant les phénomènes économiques; technique qui utilise ce traitement.

1 (…) les normes de l'économétrie moderne permettent de prévoir une modification de la structure de la demande, qui résulterait avant tout des rapports salaires-prix.

L.-V. Vasseur, J.-J. Bimbenet, et M. Hillairet, les Industries de l'alimentation, p. 48.

2 (…) en économétrie, les spécialistes soulignent souvent l'écart qui subsiste, à leurs yeux, entre le « modèle » mathématique et le « schéma expérimental », un modèle sans relations suffisantes avec le concret n'étant alors qu'un jeu de relations mathématiques, tandis qu'un modèle épousant le détail du schéma expérimental peut prétendre à atteindre le rang de structure « réelle ».

J. Piaget, Épistémologie des sciences de l'homme, p. 286 (1970).

❖

DÉR. Économétrique.

Encyclopédie Universelle. 2012.